Time Complexity: The Time complexity of an algorithm quantifies the amount of time taken by an algorithm to run as a function of the length of the string representing the input. The time complexity of an algorithm is commonly expressed using big O notation which excludes coefficients and lower order terms. When expressed this way, the time complexity is said to be described asymptotically, i.e., as the input size goes to infinity. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, where an elementary operation takes a fixed amount of time to perform. Thus the amount of time taken and the number of elementary operations performed by the algorithm differ by at most a constant factor.
Space Complexity: SPACE is the computational resource describing the resource of memory space for a deterministic Turing machine. It represents the total amount of memory space that a "normal" physical computer would need to solve a given problem with a given algorithm. It is one of the most well-studied complexity measures, because it corresponds so closely to an important real-world resource: the amount of physical computer memory needed to run a given program.
To analyses the given algorithm we need to know on what inputs the algorithm is taking less time(performing well) and on what inputs the algorithm is taking huge time. We have already seen that an algorithm can be represented in the form of an expression.
We can represent an algorithm with multiple expressions and they can be the worst case , average case and best case
1. Worst Case:
• Defines the input for which the algorithm takes huge time.
• Input is the one for which the algorithm runs the slower.
2. Average Case:
• Provides a prediction about the running time for the algorithm
• Assumes that the input is random
Lower bound<= average bound <= upper bound
For a given algorithm, we can represent best, worst, average cases in the form of expressions. As an example, let f(n) be the function which represents the given algorithm.
F(n)= n2 + 600, for worst case
F(n)= n + 100n + 600 , for best case
Similarly , for average case too. The expression defines the inputs with which the algorithm takes the average running time(or memory).
3. Best Case:
• Defines the input for which the algorithm takes lowest time.
• Input is the onre for which the algorithm runs the fastest.
How to compare algorithm
1. Execution Time: How fast is your computer depends on execution of a program
2. Number of statements: number of statements directly depend upon the number of lines
3. Ideal solution: Let us assume that we expressed running time of given algorithm as a function of the input size n and compare these different functions corresponding to running times. This kind of comparison is independent of machine time and programming style etc.
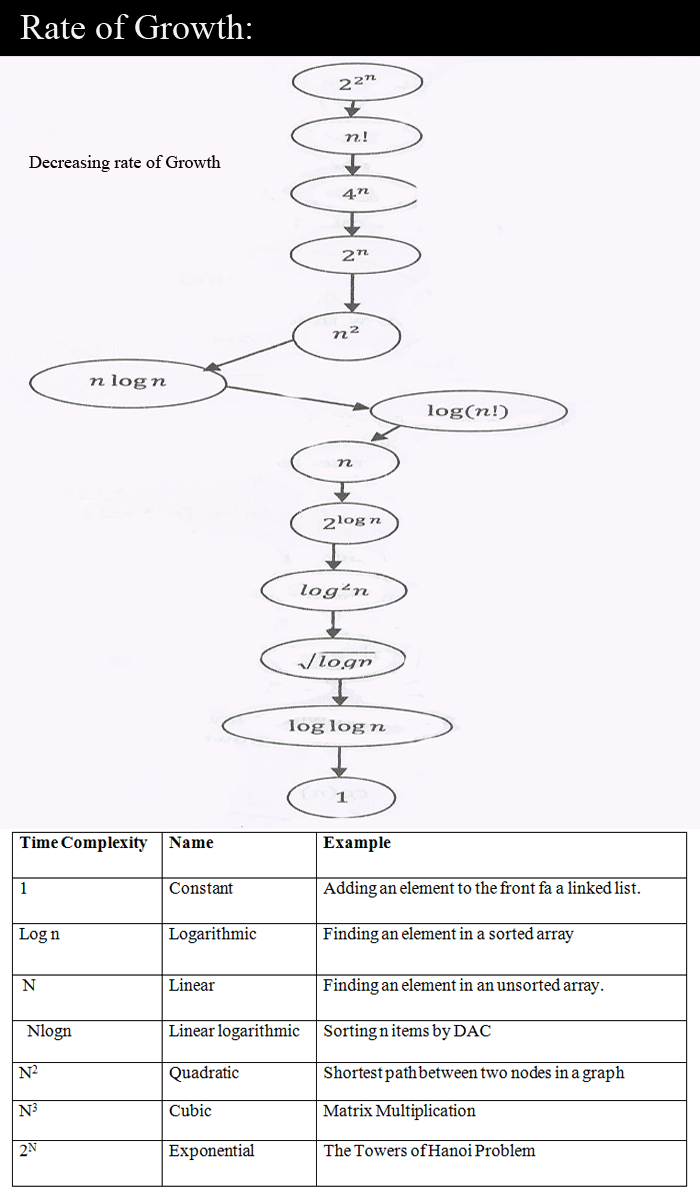
What is rate of growth: The rate at which the running time increases as a function of input is called rate of growth. Let us assume that you went to a shop for buying a car and a cycle. If you friend sees you there and asks what you are buying then I ngeneral we say a buying a car. This si because , cost of car is too big compared to cost of cycle.
Similarly , if we have a equation like n4+n3+2n2+100 so we will ignore the all the low order terms and pick only n4(they all comes in power of n.).
This is the pattern of Rate of Growth. In the below content you can see the decreasing rate of growth with some examples.
Algorithm Analysis:
Efficiency of an algorithm can be analyzed at two different stages, before implementation and after implementation, as mentioned below −
• A priori analysis − This is theoretical analysis of an algorithm. Efficiency of algorithm is measured by assuming that all other factors e.g. processor speed, are constant and have no effect on implementation.
• A posterior analysis − This is empirical analysis of an algorithm. The selected algorithm is implemented using programming language. This is then executed on target computer machine. In this analysis, actual statistics like running time and space required, are collected.
We shall learn here a priori algorithm analysis. Algorithm analysis deals with the execution or running time of various operations involved. Running time of an operation can be defined as no. of computer instructions executed per operation.
Algorithm Complexity:
Suppose C is an algorithm and n is the
size of input data, the time and space used by the Algorithm C are the
two main factors which decide the efficiency of C.
• Time Factor − The time is measured by counting the number of key operations such as comparisons in sorting algorithm
• Space Factor − The space is measured by counting the maximum memory space required by the algorithm.
The
complexity of an algorithm f(n) gives the running time and / or storage
space required by the algorithm in terms of n as the size of input
data.


