Finding Example, Theory, Concept, Algorithm
25 December, 2016
Theory:
To find the maximum and minimum value into an array of items it is not difficult. There are not many options to do that. The most natural approach is to take the first item and to compare its value against the values of all other elements. Once we find a smaller element we continue the comparisons with its value. Finally we find the minimum and vice versa for maximum.
Finding Minimum and Maximum value can be done by Divide and Conquer method but it can be solve by other method too.
If the list has more than two elements, P has to be divided into smaller instances. For example, we might divide P into the two instances P1 = (n/2,a[1],….,a[n/2]) and P2 = (n - n/2,a[n/2 + 1],….,a[n]). After having divided P into two smaller sub problems, we can solve them by recursively invoking the same divide and conquer algorithm.
Now the question is How can we combine the Solutions for P1 and P2 to obtain the solution for P? If MAX(P) and MIN(P) are the maximum and minimum of the elements of P, then MAX(P) is the larger of MAX(P1) and MAX(P2) also MIN(P) is the smaller of MIN(P1) and MIN(P2).
here we are using DAC method where we divide all the values form Top to bottom .
It helps us to find the value but it will take some space .
On the other hand there is another method to get solution is comparison.
MaxMin is a recursive algorithm that finds the maximum and minimum of the set of elements {a(i),a(i+1),…,a(j)}. The situation of set sizes one (i=j) and two (i=j-1) are handled separately. For sets containing more than two elements, the midpoint is determined and two new sub problems are generated. When the maximum and minimum of this sub problems are determined, the two maximum are compared and the two minimum are compared to achieve the solution for the entire set.
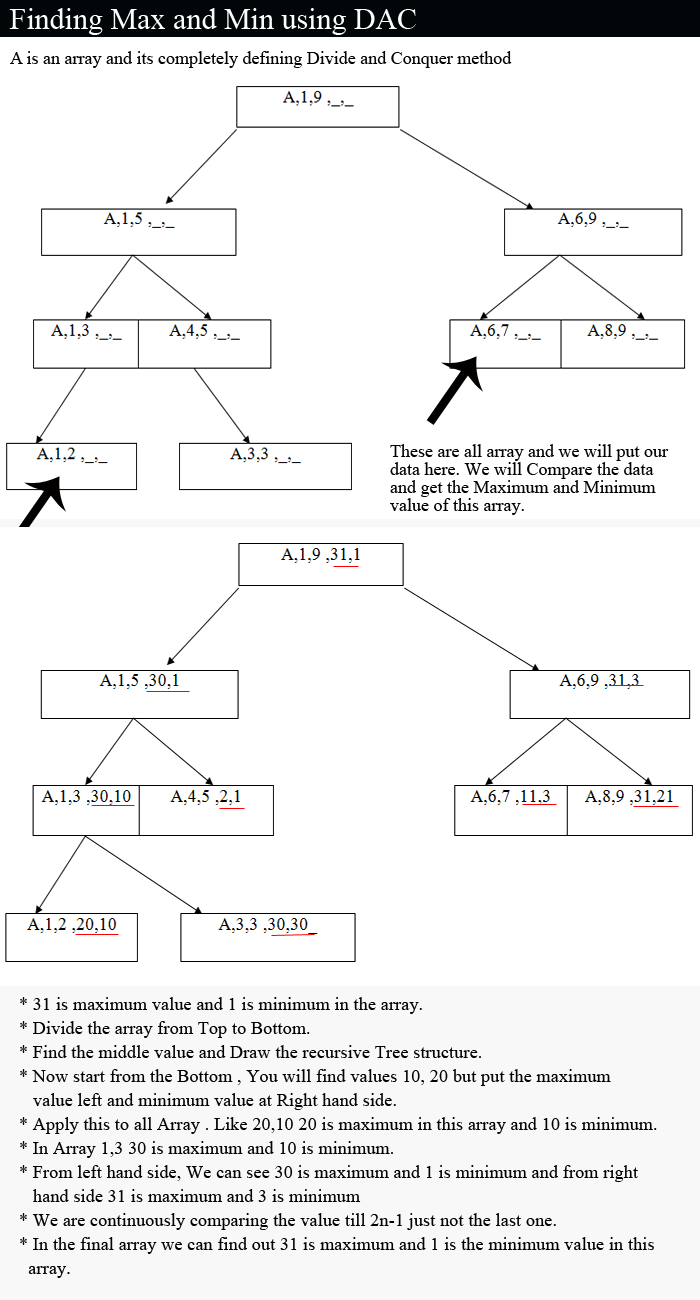
Below We have solved the problem with Divide and Conquer method.
The procedure is initially invoked by the statement MaxMin(A,n,x,y). for this algorithm each node has four items of information: i, j, max, min. Suppose we simulate MaxMin on the following nine elements:
x is maximum value and y is minimum .
n is array , i is first value and j is last value.
We have to compare the values in an array and put it into the order.
a: [1] [2] [3] [4] [5] [6] [7] [8] [9]
10 20 30 1 2 3 11 31 21
A good way of keeping track of recursive calls is to build a tree by adding a node each time a new call is made. On the array a[ ] above, the following tree is produced below
1) Finding maximum and minimum in given array:-
Let Input = 10,20,30,1,2,3,11,31,21
Output =
max=31,min=1
Solution:
2) Finding maximum and minimum in given array:-
Let Input = 22 , 13 , -5 , -8 , 15 ,60 ,17 , 31, 47
Output =
max=60,min=-8
SEE the next chapter for solution:
Till den have fun..Bye TC
