Asymptotic Notation

Learn Big O , Omega and Theta Notations

3 November, 2016     

Asymptotic Notation :- It’s a determination of order of magnitude of a statement. Asymptotic Notations are
languages that allow us to analyze an algorithm’s running time by identifying its behavior as the input size for the algorithm increases. This is also known as an algorithm’s growth rate. Does the algorithm suddenly become incredibly slow when the input size grows? Does it mostly maintain its quick run time as the input size increases?  Asymptotic Notation gives us the ability to answer these questions. To get the most from any program , we need to follow some structure and need to find out the notation of the problem.
Asymptotic notation can be categorized into three notations and they are as follows:
 Big-O-Notation:- This notation gives the tight upper bound of the given function and its represented as f(n) = O(g(n)).

 Let f(n) and g(n) be two positive functions then  f(n) = O(g(n))
 f(n) is a order of g(n).  
 f(n) ≤ cg(n)
There exist constant c>0, n0>0 such that f(n) <= cg(n) for all n >=n0
 F(n) is better than g(n) because it has best complexity.  
 In simple word at larger values of n , the upper bound of f(n) is g(n).
 for eg: f(n) =  n4 +100n2+789 then n4 is g(n)  and it means g(n) gives the maximum rate of growth for f(n).   In gneral , we discard lower values of n. That means the rate of growth at lower values of n is not important. In the below figure, n0   is the point from which we need to consider the rate of growths for a given algorithm.
 In fig(b) we can see the growth of the g(n) function.
 Upper bound {worst case}
    A=n,B=n2 relation??
    A is order of B,0(B).

Omega-Ω-Notation :-  This notation gives the tight lower bound of the given function and its represented as f(n) = Ω (g(n)).

 Let f(n) and g(n) be two positive functions then      f(n) ≥ cg(n)
 g(n) is a order of f(n).  
 f(n) ≥ cg(n)
 There exist constant c>0, n0>0 such that f(n) >= cg(n) for all n >=n0
 G(n) is better than f(n) because it has best complexity.  
  In simple word at larger values of n , the lower bound of f(n) is g(n).

                                            n, n ≥ n0
                                    Lower bound {Best case}

Theta-θ-Notation :-
This notation decides whether the upper and lower bounds of a given function(algorithm)
Are same or not. The average running time of algorithm is always between lower bound and upper bound . If the upper bound and lower bound gives the same result then it is theta notation.
For eg: f(n)= 100n + n and its tight upper bound  g(n) is O(n). In this example , the best and worst case complexity is same and as result , the average case will also be same.
In fig (a) , you can see both functions have same rate of growth.
f(n) = Ѳ(g(n))
                                    Lower & Upper bound {Average case}

     Analogies :-
               O                   Ω                     θ                   ○                 ω
               ≤                     ≥                     =                    <                 >
         Upper            Lower              Equal            Not            Not
        Bound            Bound              (both)         Tightly        Tightly
                                                                                U.B             L.B

Cases of Time Complexity
             a)  Worst Case      -    O
             b)  Best Case         -    Ω
             c)  Average Case   -    o & Ω &θ.

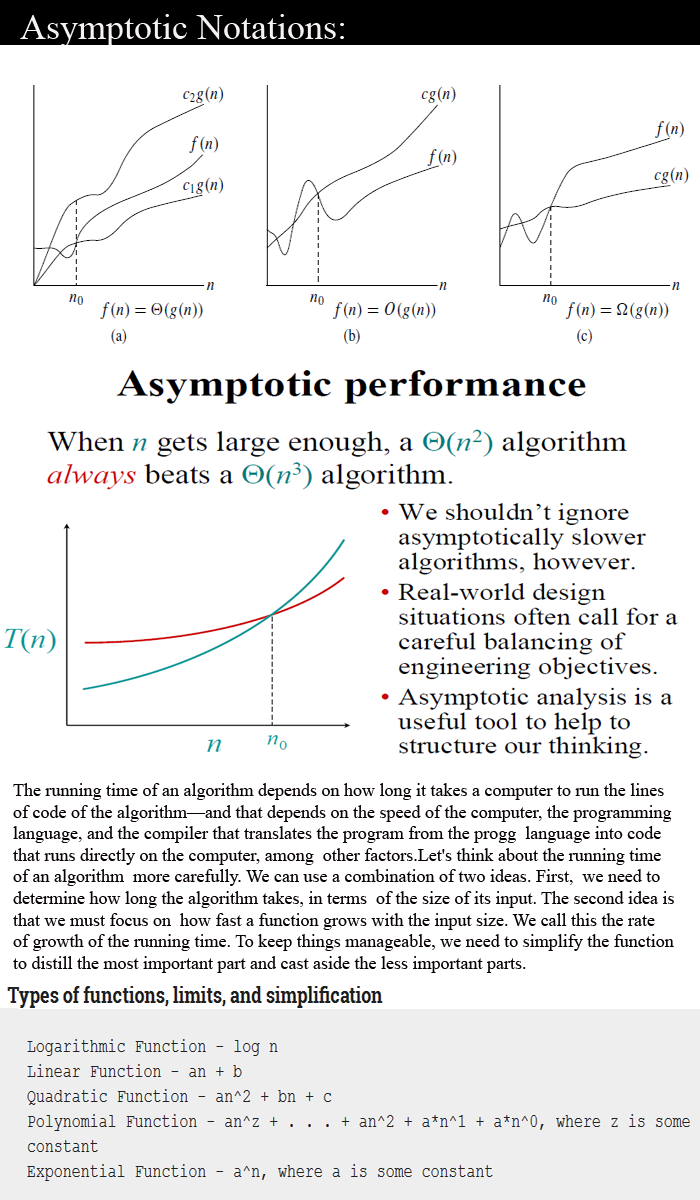
These are all three categories of Asymptotic Notation. Further we will see some examples based on Asymptotic Notations. As you can see , we

have learnt lot of things of Algorithm . These all concepts are very basic but very important to move ahead.

I m reminding you once again still we are in very Basic concept of Design and Analysis of algorithm and already learnt How can we find out the time complexity of any programs.

Time Complexity varies according to questions and other factors but the method should be same for all.

Next we will learn Amortized Algorithm so till den have fun and keep visiting my website Thanx..