Examples based on substitution method and Recursive calls
20 November, 2016
Ex-2. T(n) = T(n-1) + n if n>1
= 1 if n= 1
Sol- T(n) = T(n-1) + n
= T(n-2) +(n-1) +n
= T(n-3) + T(n-2)+(n-1)+n
…. ….. …. …. (n-1) times
=T(n-(n-1)+(n-(n-2)+…..(n-2)+(n-1)+n))
=T(1)+2+3+……..n
= (n(n+1))/2 = θ(n²)
Ex-3- T(n) = n*T(n-1) if n>1
= 1 if n=1
Sol= T(n) = n* T(n-1)
= n*(n-1)*T(n-2)
= n*(n-1)*(n-2)*T(n-3)
…………….. Repeat (n-1) times
= n*(n-1)*(n-2)*………T((n)-(n-1))
= n*(n-1)*(n-2)*………(n)-(n-2)*T(1))
= o(n^n).
Ex4- T(n) = T(n-1) + 1/n if n>1
=1 if n=1
Sol- = T(n-1)+1/n
=T(n-2) + 1/n-1+ 1/n
= n-1 times
= T(n-(n-1)) + 1/n-(n-2) + 1/n-(n-3)+….+ 1/n
=1/1+1/2+1/3+……1/n
= log(n)
=O(logn)
Ex-5- T(n)= T(n-1) + logn if n>1
= 1 n=1
Sol= T(n-1) + logn
[t(n-2)+log(n-1)]+ logn
T(n-3)+log(n-2)+log(n-1)+logn
……repeat (n-1 )times
T(1)+ log[n-(n-2)]+ log[n-(n-3)]+ .. . + logn
1 + log(2)+log(3) + log 4 …+ logn
1 + log(2.3.4….n)
1+log(n!)
nlogn
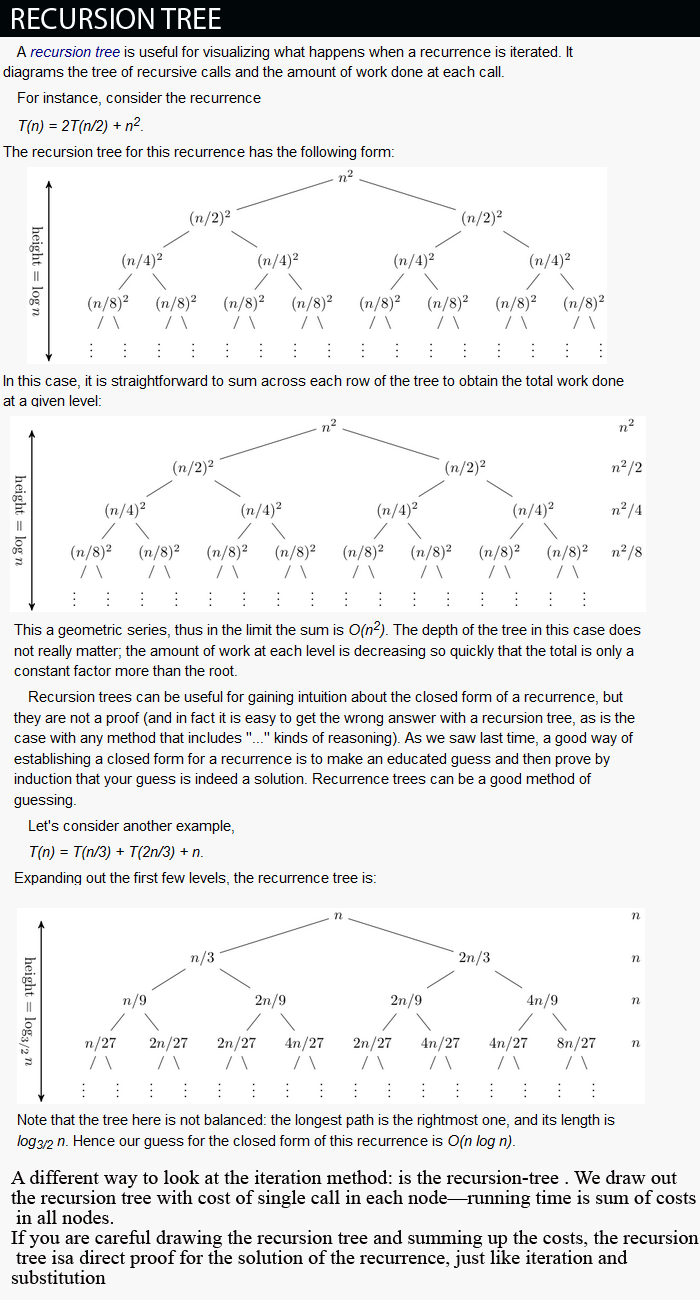
The recursion tree method is good for recursive execution of an algorithm. The recursion-tree method can be unreliable, generating guesses for the substitution method.
The recursion-tree method promotes intuition,just like any method that uses ellipses (…).
Next we will start Divide and Conquer Method..
Till den have fun ..
