Every concept need full knowledge of problem or requirement and then we can solve the problem.
To solve any problem either its related to any field , we need to make plan and that plan in terms of computer recognized as Algorithm. Like we want to make a tea so to get all resources like vessel, water, milk etc and in C programming we need to collect all things like variable, keywords etc and how we will get the result that is our algorithm. We can also view an algorithm as a tool for solving a well-specified computational problem
An algorithm is any well-defined computational procedure that takes some value, or set of values, as input and produces some value, or set of values, as output. An algorithm is thus a sequence of computational steps that transform the input into the output.
Analysis of algorithm and Properties of algorithm
The Analysis of algorithms is the determination of the amount of resources (such as time and storage) necessary to execute them. Most algorithms are designed to work with inputs of arbitrary length. Usually, the efficiency or running time of an algorithm is stated as a function relating the input length to the number of steps or storage locations
Run-time analysis
Run-time analysis is a theoretical classification that estimates and anticipates the increase in running time (or run-time) of an algorithm as its input size (usually denoted as n) increases. Run-time efficiency is a topic of great interest in Engineering of CS A program can take seconds, hours or even years to finish executing, depending on which algorithm it implements .
Running time
• The running time depends on the input: an already sorted sequence is easier to sort.
• Parametrize the running time by the size of the input, since short sequences are easier to sort than long ones.
• Generally, we seek upper bounds on the running time, because everybody likes a guarantee.
Analysis of algorithms typically focuses on the asymptotic performance, particularly at the elementary level, but in practical applications constant factors are important, and real-world data is in practice always limited in size. The limit is typically the size of addressable memory, so on 32-bit machines 232 = 4GB and on 64-bit machines 264 = 16 GB. Thus given a limited size, an order of growth (time or space) can be replaced by a constant factor, and in this sense all practical algorithms are O(1) for a large enough constant, or for small enough data.
This interpretation is primarily useful for functions that grow extremely slowly: (binary) (log*) is less than 5 for all practical data (265536 bits); (binary) log-log (log log n) is less than 6 for virtually all practical data (264 bits); and binary log (log n) is less than 64 for virtually all practical data (264 bits).
An algorithm with non-constant complexity may nonetheless be more efficient than an algorithm with constant complexity on practical data if the overhead of the constant time
algorithm results in a larger constant factor, e.g., one may have so long as and For large data linear or quadratic factors cannot be ignored, but for small data an asymptotically inefficient algorithm may be more efficient. This is particularly used in hybrid algorithms like Timsort which use an asymptotically efficient algorithm but switch to an asymptotically inefficient algorithm for small data, as the simpler algorithm is faster on small data.
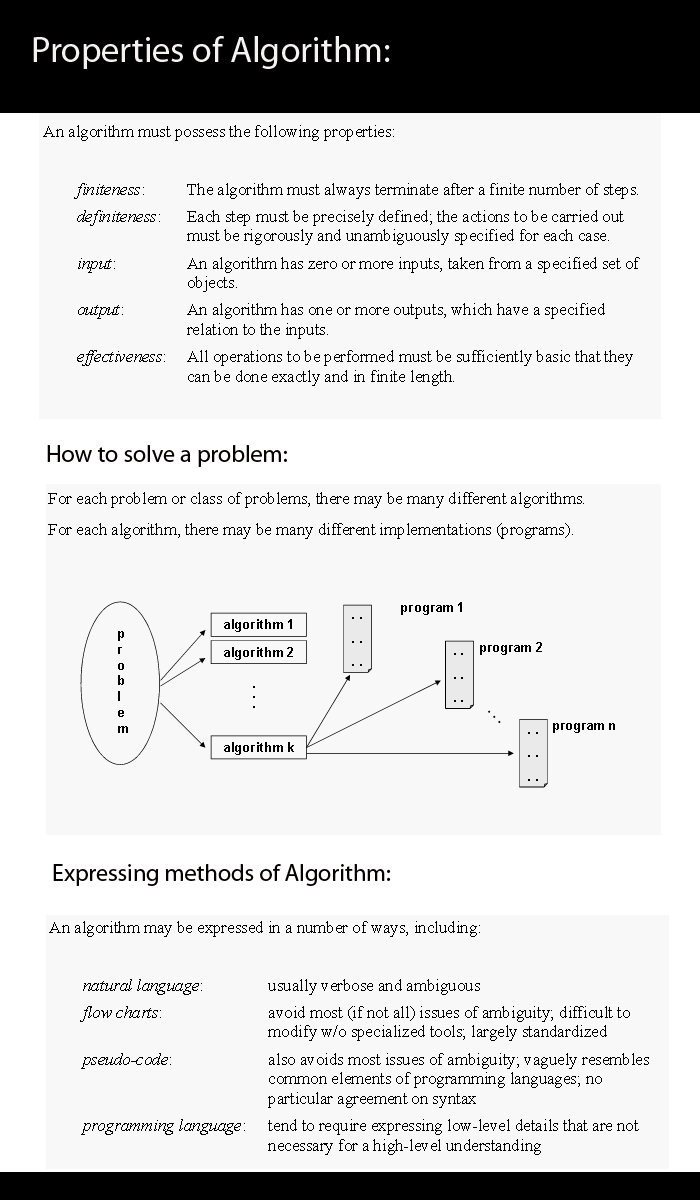
Properties of Algorithm:
1. It should take finite time
2. Every step in the algorithm should be unambigous.
3. In the algorithm , every step should perform at least one task.
4. Inputs can be vary but there should be one output
5. There should be a relation between in two steps.
In next chapter , we will start with Types of Complexity


